Algoritmos de aprendizaje sin supervisión: una técnica clave en el análisis de datos

Los algoritmos de aprendizaje no supervisado son ampliamente utilizados en minería de datos y análisis estadístico para encontrar grupos en datos sin etiquetas. K-means es uno de los algoritmos más conocidos. Identifica el número de centros de clúster y se usa para clasificar comportamientos. La selección adecuada de atributos puede mejorar la clusterización. Las aplicaciones de los algoritmos de agrupamiento son numerosas, desde segmentación de imágenes hasta la agrupación de clientes de diversas marcas.

Algoritmos de aprendizaje automático no supervisado

Los algoritmos de aprendizaje automático no supervisado se utilizan para encontrar grupos en datos no etiquetados. El problema de agrupamiento es una tarea común en la exploración de minería de datos y en el análisis de datos estadísticos, y existen miles de algoritmos que resuelven este problema de optimización.

El problema de agrupamiento

El problema de agrupamiento se refiere a la tarea de dividir un conjunto de datos en grupos o clústeres, en la que se minimice la variación dentro del grupo y se maximice la variación entre los grupos. Esta tarea es importante porque ayuda a descubrir patrones ocultos en los datos y a simplificar su análisis.

Algoritmos de agrupamiento

Existen varios algoritmos de agrupamiento, cada uno con sus propias fortalezas y debilidades. Estos algoritmos incluyen el algoritmo K-means, Mean Shift, DBSCAN y el clustering jerárquico. La selección adecuada del algoritmo depende de la naturaleza de los datos y del objetivo que se quiera alcanzar. El proceso de agrupamiento es iterativo e interactivo, y la ingeniería de datos y de características es crucial. Se deben identificar los atributos principales que describen los datos para lograr una mejor clusterización.

K-means: Algoritmo de aprendizaje no supervisado

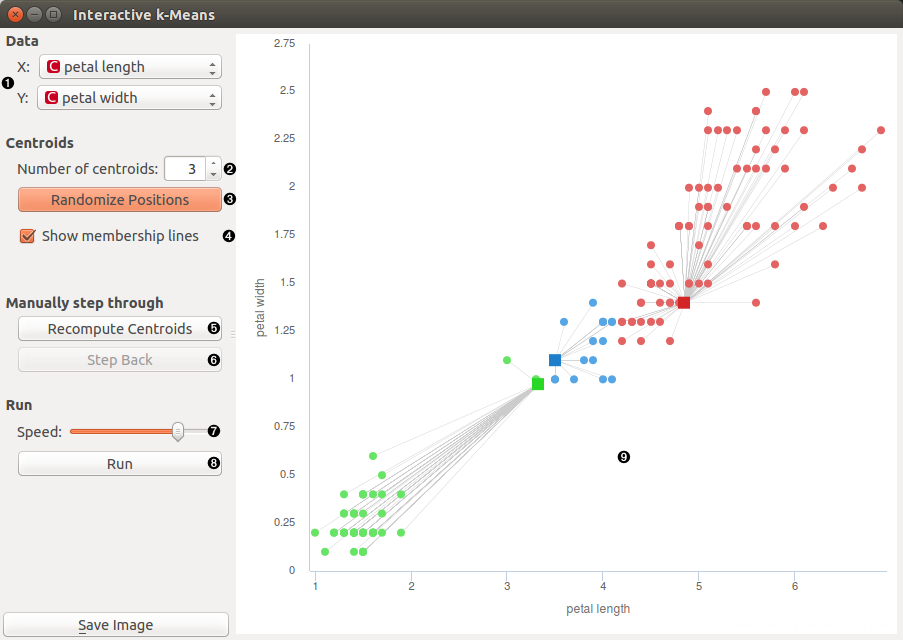
K-means es uno de los algoritmos de aprendizaje no supervisado más conocidos, utilizado para la agrupación de datos sin etiquetas. Este algoritmo se basa en la identificación de centros de clúster donde se agrupan los datos, teniendo en cuenta la distancia entre ellos y la función objetivo. 

Funcionamiento básico del algoritmo

K-means funciona de manera iterativa, comenzando con una inicialización aleatoria de centros de clúster y una asignación de datos a cada centro. A continuación, se ajustan los centros según los datos asignados, y se repite el proceso hasta que los centros ya no cambian.

K-means clustering en detalle

El algoritmo K-means utiliza la distancia euclidiana para medir la distancia entre los datos y los centros de clúster. La función objetivo del algoritmo es minimizar la suma de las distancias cuadradas entre los datos y sus respectivos centros de clúster. El número de centros de clúster inicialmente es especificado por el usuario, lo que puede afectar el resultado final de la agrupación. Asimismo, los valores atípicos pueden afectar la calidad de la clusterización obtenida. 

Ejemplo práctico de clusterización con K-means

Supongamos que se tiene un conjunto de datos en bruto relacionados a los juegos Centroamericanos que se celebran actualmente en El Salvador. Con K-means se pueden agrupar los jugadores en diferentes posiciones como, por ejemplo, atletismo, nadadores, gimnastas, tiro con arco y flecha. Los datos se normalizan y se aplican cuatro centros (es como un ejemplo pueden existir + o -) de clúster para la clusterización. Una vez ejecutado el algoritmo, se obtiene la agrupación de los jugadores en los distintos centros de clúster. Se puede observar si efectivamente se han agrupado según las características adecuadas.

Otros algoritmos de aprendizaje no supervisado

Además del algoritmo de aprendizaje no supervisado K-means, existen otros algoritmos utilizados en la agrupación de datos sin etiquetas. Algunos de ellos son Mean Shift, DBSCAN y Clustering jerárquico.

Mean Shift

Mean Shift es un algoritmo de agrupamiento no paramétrico, que es utilizado para encontrar los modos de densidad en una distribución de probabilidad. 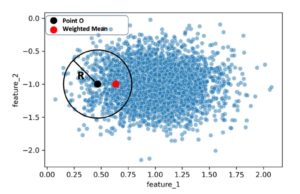Este algoritmo comienza por una selección aleatoria de una ubicación en el espacio de búsqueda y luego se mueve hacia los picos de densidad hasta que no hay más movimientos posibles. En lugar de definir previamente el número de grupos, el algoritmo Mean Shift encuentra la cantidad de grupos de datos automáticamente. Es probable que haya observado que en la gráfica previa, el radio ‘R’ del círculo negro reviste gran relevancia a la hora de definir la región local. De hecho, el radio es el parámetro primordial y único en el algoritmo de desplazamiento medio, a este se le denomina «ancho de banda».

DBSCAN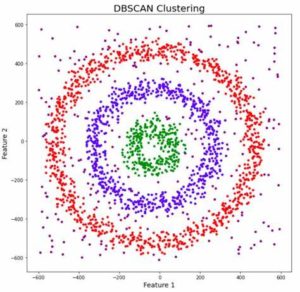

DBSCAN es otro algoritmo de aprendizaje no supervisado que se utiliza para la agrupación de datos. DBSCAN se basa en densidades y considera un grupo como una región densa de datos. El algoritmo comienza tomando un punto de datos y encuentra todos los puntos que están dentro de una distancia definida. Si la cantidad de puntos es mayor que el umbral, entonces se considera un grupo y el algoritmo se repite hasta que todos los puntos han sido considerados.

Clustering jerárquico

El Clustering jerárquico es un método de agrupamiento que construye una jerarquía de grupos. Se empieza con cada objeto en su propio grupo y se van fusionando grupos similares hasta que sólo queda un grupo. Este algoritmo puede ser aglomerativo, comenzando con grupos pequeños y fusionándolos en grupos más grandes, o dividiéndose, comenzando con un grupo único y dividiéndolo en grupos más pequeños. En detalle lo explico a continuación: 

Aglomerativo, es una estrategia ascendente donde el algoritmo inicia considerando cada punto de datos como un clúster individual y luego los combina progresivamente hasta que solo queda un único clúster.

Divisivo, sigue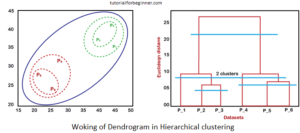 un enfoque de arriba hacia abajo, el algoritmo divisivo se posiciona en el extremo opuesto del algoritmo aglomerativo. Comienza con un solo clúster y procede a dividirlo hasta que cada punto de datos se convierte en un clúster independiente.

Algoritmos de agrupamiento basados en densidad

Los algoritmos de agrupamiento basados en densidad son una opción que se utiliza en el aprendizaje automático no supervisado, en especial en minería de datos, para identificar clústeres con densidades que superan cierto umbral. Esta técnica es útil en aplicaciones con conjuntos de datos donde la forma y el tamaño de los clústeres no están definidos de antemano.

Ejemplos de algoritmos de agrupamiento basados en densidad

• DBSCAN: Density-Based Spatial Clustering of Applications with Noise. Este algoritmo detecta clústeres a través de la densidad de los datos. Es decir, se toma en cuenta la cantidad de datos en ciertas áreas y se busca que se cumpla un umbral de densidad para poder considerarlos un clúster. Este algoritmo tiene la peculiaridad de que puede identificar ruido como un clúster aparte.
• HDBSCAN: Hierarchical Density-Based Spatial Clustering. Es una versión mejorada de DBSCAN, permite detectar clústeres de diferentes densidades, y tiene la capacidad de construir una jerarquía de clústeres.
• OPTICS: Ordering Points To Identify the Clustering Structure. Es un algoritmo que permite la identificación de clústeres de diferentes densidades sin tener que evaluar diferentes parámetros, y es capaz de detectar clústeres que no son separables espacialmente por no cumplir una densidad mínima.

Diferencias entre algoritmos de agrupamiento basados en densidad y K-means

La principal diferencia entre los algoritmos de agrupamiento basados en densidad y K-means es la forma en que definen los clústeres. Mientras que K-means utiliza la distancia euclidiana para identificar los centros de los clústeres, los algoritmos de agrupamiento basados en densidad utilizan umbrales de densidad y conectividad de los puntos. Además, los algoritmos de agrupamiento basados en densidad tienen la capacidad de detectar ruido y clústeres deformados y de diferentes densidades.

En general, la elección entre el uso de un algoritmo de agrupamiento basado en densidad o K-means dependerá del conjunto de datos y del tipo de clústeres que se busquen identificar. Si los clústeres son muy diferentes en densidad y se necesita detectarlos con precisión, los algoritmos de agrupamiento basados en densidad pueden ser la mejor opción.

Clasificación no supervisada y clusterización

Modelos de mezcla Gaussiana

La clasificación no supervisada se refiere a la agrupación de objetos sin utilizar etiquetas o clases de entrenamiento. La clasificación estadística se basa en la mezcla de modelos y es una forma de clasificación no supervisada utilizada en el análisis de datos. La mezcla de modelos se basa en la suposición de que los datos se distribuyen en múltiples formas o a través de diferentes subgrupos. La mezcla de modelos de Gauss, también conocida como modelo de mezcla Gaussiana, es una técnica de clasificación no supervisada comúnmente utilizada en la estadística y el aprendizaje automático. Este modelo asume que los datos se distribuyen en múltiples formas y las combinaciones de distribuciones Gaussianas son utilizadas para generar los modelos.

Análisis de grupos de datos

El análisis de grupos de datos es un proceso de clasificación en el que los objetos se agrupan en categorías basadas en sus similitudes. El análisis de grupos de datos se utiliza en la agrupación de datos no etiquetados en un esfuerzo por identificar patrones o grupos lógicos dentro de los datos. El análisis de grupos de datos es un componente clave de la clasificación no supervisada y se utiliza en el aprendizaje automático para la segmentación de clientes, la agrupación de documentos y la segmentación de imágenes, entre otras aplicaciones.

Identificación de la clusterización adecuada

Existen varios métodos y técnicas para identificar la clusterización adecuada en la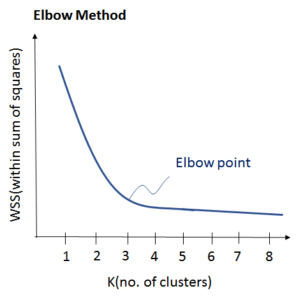 clasificación no supervisada. Una forma común de hacerlo es observando el dendrograma, también conocido como diagrama de árbol jerárquico. El dendrograma visualiza la interdependencia de las similitudes entre los elementos clasificados. Otra forma es el criterio de Elbow, que se basa en el número de clusters y la suma de las varianzas. La identificación de la clusterización adecuada es crucial para garantizar que los grupos o clusters sean significativos y útiles en la interpretación de los datos.

• La mezcla de modelos de Gauss es una técnica común de clasificación no supervisada utilizada en el análisis de datos
• El análisis de grupos de datos se utiliza en la agrupación de datos no etiquetados en un esfuerzo por identificar patrones o grupos lógicos dentro de los datos
• Existen varios métodos y técnicas para identificar la clusterización adecuada en la clasificación no supervisada

Mejora de la clusterización con atributos

La clusterización es una técnica importante en el análisis de datos, sin embargo, la calidad de los resultados depende en gran medida de la selección de atributos relevantes. Es importante elegir bien aquello que se desea medir en los datos para que el resultado obtenido sea más significativo y útil. A continuación, se presentan tres aspectos clave para mejorar la clusterización con atributos.

Importancia de los atributos

Los atributos son medidas que se utilizan para describir el fenómeno que se desea analizar. Es importante tener en cuenta cuáles son los atributos más relevantes para la clusterización, ya que no todos tienen la misma importancia. Para seleccionar los atributos relevantes se deben tener en cuenta las características del conjunto de datos a analizar y los objetivos que se persiguen en la clusterización.

Es importante no incluir atributos redundantes o que no proporcionen información relevante para el análisis. Además, el número de atributos debe ser manejable por el sistema de clusterización, ya que si hay muchos atributos, puede resultar difícil encontrar grupos que tengan sentido.

Selección de atributos relevantes

Para seleccionar los atributos más importantes se pueden utilizar técnicas de reducción de dimensionalidad, que permiten transformar los datos originales en un conjunto de datos de menor dimensión, manteniendo la mayor parte de la información y eliminando la redundancia.

Entre las técnicas más utilizadas se encuentran Análisis de Componentes Principales (PCA), Análisis Discriminante de Fisher (FDA) y Análisis de Correlación Canónica (CCA), entre otros. La elección de la técnica dependerá del conjunto de datos y de los objetivos perseguidos.

Atributos y su impacto en la clusterización

La selección de atributos tiene un impacto directo en la calidad de los resultados de la clusterización. Los atributos seleccionados deben permitir una clusterización adecuada, de tal manera que se puedan identificar grupos homogéneos y bien diferenciados.

Es importante tener en cuenta que la selección de atributos adecuada puede variar dependiendo del conjunto de datos y de los objetivos perseguidos. Por lo tanto, es importante llevar a cabo un análisis detallado de los atributos para obtener los resultados de clusterización más precisos y útiles.

• Los atributos son medidas que se utilizan para describir el fenómeno que se desea analizar.
• Es importante elegir bien cuáles son los atributos más relevantes para la clusterización para que el resultado sea más significativo y útil.
• Los atributos redundantes o que no proporcionen información relevante deben ser eliminados.
• Se pueden utilizar técnicas de reducción de dimensionalidad para seleccionar los atributos más importantes.
• La elección de la técnica dependerá del conjunto de datos y de los objetivos perseguidos.
• Los atributos seleccionados deben permitir una clusterización adecuada.
• La selección de atributos adecuada puede variar dependiendo del conjunto de datos y de los objetivos perseguidos.

Aplicaciones de los algoritmos de agrupamiento

Los algoritmos de agrupamiento se utilizan ampliamente en diversos campos de la industria, y a continuación se presentan algunas aplicaciones específicas de estos algoritmos:

Ejemplos de aplicaciones

• Motores de recomendación: los motores de recomendación utilizan la clusterización para agrupar a los usuarios según sus preferencias y ofrecer recomendaciones personalizadas de productos o contenido basados en su historial de navegación.
• Segmentación de imágenes: la clusterización se utiliza para segmentar imágenes en diferentes partes, lo que puede ser útil en la mejora de la resolución de la imagen o en la identificación de partes de la imagen para su posterior análisis.
• Agrupación de documentos: los algoritmos de agrupamiento se utilizan para agrupar documentos similares basados en su contenido, lo que puede ser útil para la clasificación y organización de grandes volúmenes de información.
• Segmentación de clientes: en el sector bancario y del comercio electrónico, los algoritmos de agrupamiento se utilizan para identificar grupos de clientes similares en función de sus patrones de gasto y comportamiento de compra para una mejor segmentación de mercado.
• Agrupación de genes: en la biología, los algoritmos de agrupamiento se utilizan para agrupar genes similares en función de su función biológica o comportamiento en un estudio de ADN.

Sectores donde se utilizan los algoritmos de agrupamiento

• Banca: los algoritmos de agrupamiento se utilizan en la segmentación de clientes y en la identificación de fraude.
• Comercio electrónico: los algoritmos de agrupamiento se utilizan en la recomendación de productos y en la segmentación de clientes.
• Ventas: la clusterización se utiliza para la segmentación de clientes y la previsión de ventas.
• Publicidad: los algoritmos de agrupamiento se utilizan en la segmentación de mercado y la definición de objetivos demográficos.
• Deporte: los algoritmos de agrupamiento se utilizan en la evaluación de jugadores y en la identificación de patrones de juego. Y en muchísimos campos más!!

Toma decisiones basadas en datos

www.analitikacentroamerica.com